Quaestio facti. Revista Internacional sobre Razonamiento Probatorio
Quaestio facti. International Journal on Evidential Legal Reasoning
Sección: Ensayos
2024 l 6 pp. 77-100
Madrid, 2024
DOI: 10.33115/udg_bib/qf.i6.22981
Marcial Pons Ediciones Jurídicas y Sociales
© Pablo E. Navarro
© Jorge L. Rodríguez
ISSN: 2604-6202
Recibido: 22/11/2023 | Aceptado: 27/12/2023 | Publicado online: 19/01/2024
Editado bajo licencia Reconocimiento 4.0 Internacional de Creative Commons

Apuntes para una lógica de la prueba en el derecho*

Pablo E. Navarro

Lisbon Legal Theory, Lisbon Public Law, University of Lisbon
CONICET, Argentina.
pabnav@hotmail.com

Jorge L. Rodríguez

University of Mar del Plata, Argentina.
jorgerodriguez64@yahoo.com

RESUMEN: Pese al auge actual de los desarrollos teóricos respecto de la prueba de los hechos en el derecho, constituye todavía una asignatura pendiente el reconstruir adecuadamente una lógica de la prueba. En el presente trabajo se presentarán algunas ideas preliminares para una reconstrucción semejante. Suponiendo ya cumplida la producción y valoración de ciertos elementos de prueba en un proceso, se explorarán cuáles resultarían candidatos adecuados para tomar como principios básicos de una lógica de la prueba, examinando las similitudes y diferencias del sistema resultante con otros sistemas de lógicas modales con los que guarda analogías, en particular la lógica alética, la lógica deóntica, la lógica epistémica y la lógica de la verdad.

PALABRAS CLAVE: lógica de la prueba, lógica modal, razonamiento probatorio, epistemología jurídica, consecuencia lógica.

Notes for a Logic of Evidence in Law

ABSTRACT: Despite the current theoretical developments regarding the proof of facts in law, it is still an open problem to offer an adequate reconstruction of a logic of evidence. This paper presents some preliminary ideas for such a reconstruction. Starting from the assumption that the production and evaluation of certain evidence in a legal process has already been completed, it examines which candidates would be suitable as basic principles for a logic of evidence. The similarities and differences of the resulting system with other modal logic systems with which it appears to have analogies, in particular alethic logic, deontic logic, epistemic logic, and the logic of truth, are examined.

KEYWORDS: logic of evidence, modal logic, evidential legal reasoning, legal epistemology, logical consequence.

SUMARIO: 1. INTRODUCCIÓN.— 2. LOS PRINCIPIOS BÁSICOS DE UNA LÓGICA DE LA PRUEBA.— 3. LÓGICA DE LA PRUEBA Y OTROS SISTEMAS MODALES.— 4. SEMÁNTICA DE MUNDOS POSIBLES Y ESTÁNDARES DE PRUEBA.— 5. LEYES DE DISTRIBUCIÓN, TAUTOLOGÍAS Y UNA PROPUESTA DE AXIOMATIZACIÓN.— 6. CONCLUSIONES.— BIBLIOGRAFÍA.

1. Introducción

El objetivo de este trabajo es elaborar las bases de una lógica de enunciados probatorios (en adelante lógica de la prueba, LP) y explorar sus analogías y diferencias con otras lógicas modales 1. A diferencia de otros enfoques formales, que se ocupan de la prueba en términos de inducción o probabilidad con el propósito de determinar la justificación racional de un cierto enunciado fáctico 2, pretendemos mostrar qué relaciones lógicas se verifican entre enunciados probatorios. En otras palabras, nuestro interés es analizar los compromisos racionales que se asumen al admitir que está probado un cierto enunciado en un determinado proceso judicial.

Esta perspectiva nos lleva a: i) analizar si existen leyes específicas de la lógica de la prueba que sean diferentes de otras lógicas; ii) considerar en qué sentido es plausible admitir como jurídicamente probados enunciados tautológicos 3 y iii) examinar si las consecuencias lógicas de los enunciados probatorios también deben considerarse jurídicamente probadas.

En gran medida, la adecuación y utilidad de una lógica de la prueba depende de consideraciones sustantivas acerca de la naturaleza de la prueba y el razonamiento probatorio. A efectos de limitar nuestro universo de discurso asumiremos en este trabajo los postulados principales que caracterizan a la denominada concepción racionalista de la prueba. De acuerdo con esta, la justificación de la prueba de un enunciado debe regirse por los criterios de racionalidad epistémica general 4.

Por «enunciado probatorio» entendemos un enunciado de la forma «Está probado que p» (en adelante, Pp). La variable p representa una proposición 5, que puede ser considerada el contenido del enunciado probatorio Pp 6. La expresión «Está probado...» es un operador proposicional en el sentido de que, al añadirse el prefijo «Está probado» a una determinada proposición p, se genera otra proposición diferente (la proposición Pp) y esta última también puede combinarse por medio de las conectivas lógicas usuales 7.

Los enunciados probatorios que analizaremos son aquellos que cumplen con las siguientes tres características: objetividad, independencia y definitividad.

1) Objetividad: Un enunciado probatorio es objetivo en la medida en que sus valores de verdad no dependen de las creencias de los participantes en el proceso (por ejemplo, jueces, abogados, etc.). Más bien, su verdad o falsedad depende exclusivamente de los datos que las partes han introducido en el proceso, y que sirven de base o fundamento para el enunciado probatorio. En este sentido, los jueces pueden cometer errores al valorar las pruebas y al determinar los hechos relevantes del caso, aunque sus decisiones sean definitivas en el marco del proceso 8. En otras palabras, una reconstrucción objetiva de los enunciados probatorios no pretende tener en cuenta las creencias reales de los jueces u otros miembros del proceso (por ejemplo, los jurados en un proceso penal). El valor de verdad de la declaración probatoria Pp depende exclusivamente de si hay razones suficientes (es decir, razones incorporadas en el proceso) a favor de la proposición que es el contenido del enunciado probatorio 9.

2) Independencia: El valor de verdad de un enunciado probatorio como Pp es independiente de la verdad o falsedad de p. Aun suponiendo que el propósito primordial de la actividad probatoria en un proceso judicial sea la determinación de la verdad, dicha actividad debe considerarse como el medio por el cual se busca determinar la verdad en el derecho, y debido a las limitaciones de tales medios, no se puede garantizar que se logre el fin 10. Por lo tanto, debe rechazarse la existencia de una relación conceptual entre prueba y verdad, en el sentido de que esta última no es una condición necesaria ni suficiente de la primera. Podría suceder que una proposición verdadera no haya sido probada en el proceso y, a su vez, que una proposición falsa haya sido probada jurídicamente. Por consiguiente, una concepción racionalista del razonamiento probatorio rechaza que los enunciados probatorios aceptados por los jueces sean constitutivos de su verdad, o que ejemplifiquen una suerte de «verdad formal» que pueda oponerse a otra «verdad material» 11.

3) Definitividad: En un procedimiento jurídico se introducen varios enunciados probatorios que tienen por objeto servir de base para una decisión final. Estos enunciados probatorios reflejan una evaluación parcial de ciertos elementos introducidos en el proceso. Sin embargo, las disputas sobre las pruebas fácticas terminan con un enunciado probatorio definitivo en el marco de ese proceso, que se obtiene de la evaluación de todo el cuerpo de pruebas relevantes en un determinado juicio 12. Por lo tanto, se dirá que un enunciado probatorio como Pp es definitivo cuando se obtiene después del balance de razones a favor o en contra de p. Estos enunciados probatorios presuponen i) la verdad de otras proposiciones que conforman el contexto probatorio y ii) que el equilibrio de elementos de juicio a favor de p y en contra de p se inclina en el primer sentido. Más allá de la importancia de las declaraciones intermedias o provisionales, aquí solo nos interesa analizar los enunciados probatorios definitivos (concluyentes) formulados por los jueces 13.

Estas tres características de los enunciados probatorios son un criterio de selección de elementos de un conjunto bastante heterogéneo que los juristas (especialmente los jueces) utilizan en el marco de un proceso específico para justificar una determinada solución. La consideración de esas características como definitorias de la clase de enunciados probatorios aptos para una lógica de la prueba deja abierto el camino a ulteriores (y necesarios) refinamientos, que no pueden ser emprendidos en este trabajo 14. Estos refinamientos pueden provenir de diversas fuentes como, por ejemplo, i) los desarrollos contemporáneos en epistemología sobre las relaciones entre conocimiento, creencia, verdad y justificación y ii) la misma práctica jurídica 15. En otras palabras, una lógica de la prueba en el derecho es, por así decirlo, un territorio intermedio entre los desarrollos filosóficos sobre epistemología y lógica y las restricciones institucionales propias a la búsqueda de la verdad que se encuentran en el ámbito de la prueba jurídica.

2. Los principios básicos de una lógica de la prueba

En cualquier reconstrucción formal de una disciplina es importante comprender qué verdades lógicas específicas encontramos en cada uno de esos dominios. Al respecto, refiriéndose a la lógica deóntica, von Wright (1951a, p. 5) señala que «… la existencia de verdades lógicas que son peculiares a los conceptos deónticos es lo que hace interesante al estudio de la lógica deóntica». De manera similar, es posible analizar las particularidades de la lógica del razonamiento probatorio.

El razonamiento acerca de la prueba de la verdad de un enunciado en general, y de la prueba jurídica en particular, presenta aspectos peculiares que van más allá de la lógica clásica (i.e., proposicional o de predicados). La más destacada de estas particularidades es la distancia conceptual entre prueba y verdad. Mientras que en las disciplinas formales una «prueba» de un teorema implica la demostración de su verdad, en el ámbito jurídico es usual admitir que la prueba de un determinado estado de cosas no garantiza su verdad. Por esa razón, el eje central de la reconstrucción formal del razonamiento probatorio en el derecho tiene que reconocer la posibilidad de que carezcamos de una prueba para un enunciado p y su negación (~p) 16. A su vez, esta posibilidad muestra la plausibilidad de distinguir entre una negación «interna» y una negación «externa» de los enunciados probatorios, es decir, entre afirmar que está probado que p es falso (P~p) y afirmar que no está probado que p es verdadero (~Pp) 17.

A continuación, intentaremos sistematizar algunos de los aspectos más relevantes de estas distinciones a partir de tres ideas intrínsecamente relacionadas.

En primer lugar 18, considérese la ley de tercero excluido de la lógica clásica: para toda proposición p vale que p, o bien su negación (~p), es verdadera, esto es, (p ∨ ~p) es una fórmula que expresa una verdad lógica. En una lógica acerca de la prueba, la adición a nuestro lenguaje del operador P permite analizar, por ejemplo, cuál de las siguientes traducciones del principio de tercero excluido al ámbito probatorio es admisible y cuáles serían las relaciones entre ellas.

(1) Pp ∨ ~Pp (3) Pp ∨ P~p

(2) P(p ∨ ~p) (4) Pp ∨ ~P~p

De estas cuatro expresiones, (1) expresa sin dudas una verdad lógica porque se trata de una aplicación directa de la lógica proposicional a la lógica de la prueba: cualquier enunciado, incluso un enunciado probatorio (Pp) o bien es verdadero o bien no es verdadero 19. Por otra parte, como se examinará en profundidad más adelante, también (2) debería admitirse como una ley de la lógica de la prueba. Por el contrario, (3) debería descartarse como verdad lógica de LP. La razón es que parecería necesario admitir en una lógica de la prueba que con respecto a cualquier proposición p podría ocurrir que no esté probado ni que p es verdadera ni que p es falsa. La fórmula (4) resulta igualmente inadmisible porque ella es proposicionalmente equivalente a Pp → P~p, lo que equivaldría a sostener que la prueba de la verdad de una proposición implica la prueba de su falsedad, algo que parece absurdo. Es más, si (4) se admitiera como una ley lógica en LP, dado que como luego veremos Pp implica ~P~p, de ello se seguiría que (4) equivale a ~P~p 20. En consecuencia, admitir la validez de (4) conjuntamente con la validez de (3) llevaría a la absurda consecuencia de que toda proposición p debería considerarse trivialmente probada.

En segundo lugar, un análisis de los principios básicos de una lógica de la prueba debe reconocer que existe una distancia entre prueba y verdad, en el sentido de que debe considerarse consistente a un enunciado como 21:

(5) p ∧ ~Pp

Esto es, debe admitirse la posibilidad de que, pese a que una proposición sea verdadera, de acuerdo con la evidencia producida en un proceso no esté probada. Incluso debería considerarse que también es consistente:

(6) p ∧ P~p

Es decir, una proposición puede ser verdadera y, no obstante, de acuerdo con la evidencia producida en un proceso, estar justificado aceptar como probado que es falsa (o, equivalentemente, que una proposición puede ser falsa y, no obstante, estar justificado dentro de un proceso considerar probado que es verdadera) 22.

Finalmente, como ya se dijo, una idea que parece muy plausible pensando en la reconstrucción de una lógica de la prueba es que, si se encuentra probada la verdad de cierta proposición, no puede también estar probada su falsedad, y si está probada su falsedad, no puede también estar probada su verdad:

(7) Pp → ~P~p

(8) P~p → ~Pp

Por simple lógica proposicional (7) es equivalente a:

(9) ~(Pp ∧ P~p), y a

(10) ~Pp ∨ ~P~p

La fórmula (9) expresa que no es admisible tener por probada tanto la verdad como la falsedad de una misma proposición p, en tanto que (10) expresa que o bien no está probada la verdad o bien no está probada la falsedad de una proposición p. Por otra parte, también por simple lógica proposicional deberían admitirse:

(1) Pp ∨ ~Pp, y

(11) ~(Pp ∧ ~Pp)

En otras palabras, (1) expresa que un enunciado probatorio o bien es verdadero o bien es falso, y (11) que un mismo enunciado probatorio no puede ser verdadero y falso a la vez. Lo mismo vale para la prueba de la falsedad de una proposición:

(12) P~p ∨ ~P~p

(13) ~(P~p ∧ ~P~p)

Por lo tanto, Pp y ~Pp (así como P~p y ~P~p) son contradictorios entre sí: resultan mutuamente excluyentes y conjuntamente exhaustivos.

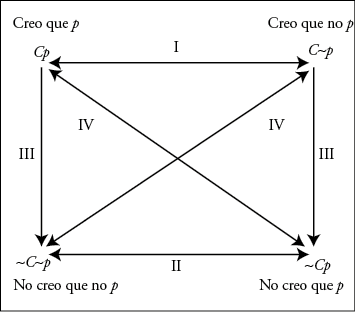
Los principios esbozados pueden esquematizarse en el siguiente cuadro:

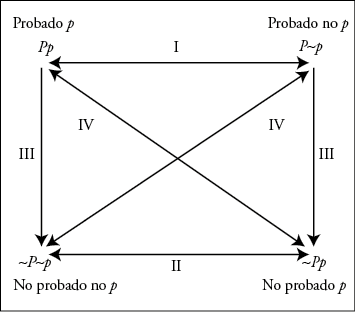
En este esquema, (I) expresa la relación de contrariedad (Pp y P~p no pueden ser ambos verdaderos, lo que está recogido en el principio [9]); (II) la relación de subcontrariedad (o bien ~Pp o bien ~P~p, lo que está recogido en el principio [10]); (III) las relaciones de subalternación (Pp implica ~P~p y P~p implica ~Pp, expresados en los principios [7] y [8]), y (IV) las relaciones de contradicción (expresadas en los principios [1], [11], [12] y [13]).

En resumen, las relaciones formales más intuitivas entre enunciados probatorios serían las siguientes:

1) El enunciado Pp es incompatible con el enunciado ~Pp. Conforme a esta intuición, la conjunción de ambos enunciados (Pp ∧ ~Pp) no puede aceptarse en LP.

2) Un mismo enunciado probatorio no puede ser simultáneamente verdadero y no verdadero. De allí se sigue que los enunciados probatorios se comportan de manera similar a la lógica clásica en el sentido de que la proposición Pp y su negación ~Pp son mutuamente excluyentes. Esto equivale a asumir Pp ∨ ~Pp como una tautología de los enunciados probatorios.

3) P~p es, en cierto sentido, la negación de Pp ya que ambos no pueden ser conjuntamente verdaderos. Dado que ~(P~p ∧ Pp) es equivalente a P~p → ~Pp, se sigue que la negación interna de un enunciado probatorio p (P~p) implica a su negación externa (~Pp ).

3. Lógica de la prueba y otros sistemas modales

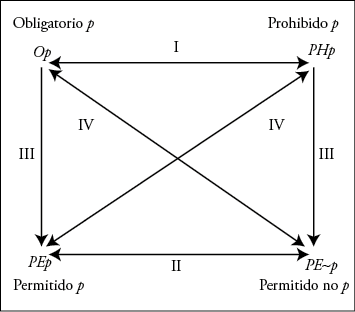
A partir de esta informal —y elemental— reconstrucción, es posible mostrar las profundas analogías que median entre la lógica de la prueba así concebida y otros sistemas lógicos. Como es sabido, las mismas relaciones indicadas en el cuadro precedente se verifican entre los juicios categóricos (o enunciados cuantificados), las modalidades aléticas, las modalidades deónticas y las modalidades propias de la lógica epistémica, tanto sea respecto del operador C (meras creencias) o del operador K (conocimiento).

Estas analogías pueden ejemplificarse en los siguientes diagramas:

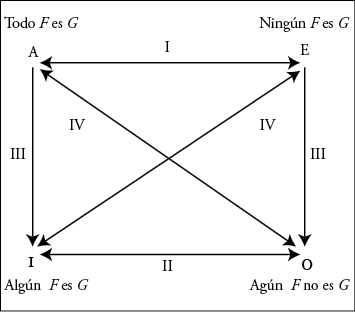
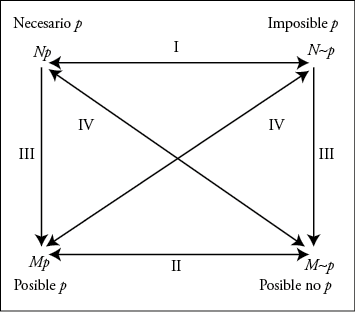
Las analogías que median entre los enunciados cuantificados, los conceptos modales aléticos, los deónticos y los epistémicos son tan estrechas que no parece que puedan ser el producto de una mera coincidencia, una suerte de «accidente filosófico» 23. Por el contrario, es tentador asumir que existe alguna razón que las justifique. Una razonable hipótesis explicativa sería suponer que la similitud deriva de que todos estos grupos son reducibles en última instancia a un único grupo fundamental. De las distintas posibilidades, la que se ha demostrado más fructífera ha sido la reducción de los conceptos modales aléticos, los deónticos y los de creencias a enunciados cuantificados. Así, los enunciados modales aléticos pueden traducirse en enunciados cuantificados por medio de la idea propuesta inicialmente por Leibniz (1672/1930, p. 466) de que la verdad de un enunciado es necesaria si ese enunciado es verdadero en todo mundo posible, y que la verdad de un enunciado es posible si al menos existe un mundo posible en el cual es verdadero.

Con mayor precisión, siguiendo a Kripke (1959, 1963), puede definirse un marco kripkeano como una estructura compuesta por tres elementos: <M, R, V>, donde M es un conjunto no vacío de mundos posibles, R es una relación diádica (que vincula dos elementos) de posibilidad relativa, a la que se califica usualmente como relación de accesibilidad, y V es una función de valuación que asigna valores de verdad al par conformado por una cierta fórmula de un lenguaje L y un elemento de M. De acuerdo con este modelo, puede decirse que p es necesariamente verdadero en un mundo m si y solo si para todo mundo posible m’ que resulta accesible respecto de m de acuerdo con R, p es verdadero en m’. Y p es posiblemente verdadero en m si y solo si existe al menos un mundo posible m’ accesible respecto de m de acuerdo con R, y p es verdadero en m’ 24. Desde un punto de vista lógico es innecesario tomar partido sobre la naturaleza de los mundos posibles: puede concebírselos como proposiciones, estados de cosas, entidades con existencia independiente, o como modos de ser que el mundo podría haber asumido si las cosas hubiesen sido distintas de como son, entre otras posibles alternativas de interpretación 25.

La idea básica para el desarrollo de un sistema de lógica deóntica sobre estas mismas bases consiste en las siguientes cláusulas de verdad para los enunciados deónticos: una norma como «Obligatorio p» (Op) sería verdadera en un mundo m si y solo si p es verdadera en todos los mundos deónticamente accesibles respecto de m de acuerdo con R, y una norma como «Permitido p» (PEp) sería verdadera en m si y solo si hay al menos un mundo deónticamente accesible respecto de m de acuerdo con R en el cual p es verdadera 26. Intuitivamente, la relación de accesibilidad deóntica R puede leerse del siguiente modo: un mundo posible m’ que satisface la relación R con el mundo m es tal que en él se cumple todo lo que es obligatorio en m, por lo que todos los mundos m’ que satisfacen esta relación con m pueden verse como mundos normativamente ideales respecto de m.

Hasta aquí todo es bien conocido. Ahora bien, ¿puede sostenerse algo similar respecto de las creencias? A partir de consideraciones de Hintikka en un clásico libro de 1962, puede proyectarse la misma idea a la lógica de creencias del siguiente modo: un agente a considera un posible número de diferentes situaciones que son consistentes con la información que posee. Siendo así, puede decirse que el agente a cree o conoce que p es verdadera si y solo si p es verdadera en todas las situaciones que considera posibles, y del mismo modo puede decirse que el agente a no cree o conoce que p es falsa si y solo si existe al menos una situación considerada posible en la que p es verdadera 27.

En el caso de los enunciados de prueba, esta idea puede también recogerse de diversas maneras: una vez producida la prueba en un proceso contamos con un conjunto de evidencias producidas y podemos considerar a ciertas hipótesis como plausibles acerca de lo acontecido, en tanto que otras quedarán descartadas como implausibles. Siendo ello así, puede decirse que está probado que una proposición p es verdadera si y solo si p es verdadera en todas las situaciones concebibles que resultan consistentes con los elementos de prueba producidos, o bien en todas las hipótesis plausibles acerca de lo acontecido. Si en cambio existe una situación concebible o hipótesis plausible en la que p es falsa, no estará probado p. De igual modo, estará probado que una proposición p es falsa si y solo si es falsa en todas las situaciones concebibles que resultan consistentes con los elementos de prueba producidos, o bien en todas las hipótesis plausibles acerca de lo acontecido. Si en cambio existe una situación concebible o hipótesis plausible en la que p es verdadera, no estará probado que p es falsa.

Como es sabido, Kripke (1959, 1963) advirtió agudamente que, en la semántica de mundos posibles, exigir la satisfacción de diferentes propiedades formales respecto de la relación de accesibilidad entre mundos da lugar a diferentes sistemas lógicos. Si no se impone ninguna restricción sobre la relación de accesibilidad, el resultado que se obtiene es un sistema lógico (el sistema K) muy débil que se caracteriza por el axioma #(A → B) → (#A → #B), donde # es cualquier operador modal. Este principio resulta válido en todos los sistemas lógicos aquí considerados 28.

En el caso de la lógica modal alética, al igual que en la lógica epistémica para el operador K (conocimiento), parece natural asumir algo más fuerte: que la relación de accesibilidad es reflexiva: (∀m (Rmm)), es decir, que todo mundo posible es accesible a sí mismo 29. Esto genera que en lógica modal alética valga el principio de que Np → p, esto es, si una proposición es necesariamente verdadera, entonces es obviamente verdadera, y el principio de que p → Mp, esto es, una proposición verdadera es posible. Del mismo modo, en la lógica del conocimiento valdrá el principio de que Kp → p, es decir, si se conoce la verdad que p, entonces p es verdadera (lo cual se corresponde con la noción usual de conocimiento como creencia verdadera justificada), y el principio p → ~K~p, esto es, si una proposición es verdadera no podría conocerse su falsedad. La razón por la cual la reflexividad de la relación de accesibilidad entre mundos garantiza la validez de estas fórmulas es que, tomando el caso del operador de necesidad, si la verdad de p es necesaria en el mundo real, entonces p es verdadera en todo mundo posible que sea accesible al mundo real, y dado que el mundo real por reflexividad será uno de esos mundos accesibles, entonces p será igualmente verdadera en el mundo real.

En este punto, la lógica de la prueba que estamos delineando parece más próxima a la lógica deóntica y a la lógica de las creencias, dado que en ninguno de los tres casos parece razonable asumir el análogo de los principios comentados en el párrafo anterior 30. Es decir, en lógica deóntica ni Op → p (la obligatoriedad de p implica su verdad) ni p → PEp (la verdad p implica su permisión) pueden admitirse como principios válidos; en lógica de creencias ni Cp → p (la creencia en la verdad de p implica su verdad) ni p → ~C~p (la verdad de p implica que no creamos en su falsedad) pueden admitirse como principios válidos, y en la lógica de la prueba ni Pp → p (si p está probada es verdadera) ni p → ~P~p (si p es verdadera no está probada su falsedad) pueden admitirse como válidos. Debido a ello, no es razonable asumir que la relación de accesibilidad en estos casos sea reflexiva. Ahora, para que en la lógica deóntica sea válido el principio de que obligatorio implica permitido (Op → PEp), en la lógica de las creencias valga el principio de que Cp → ~C~p, esto es, que la creencia en la verdad de p implica que no se puede creer al propio tiempo en su falsedad, y en la lógica de la prueba valga el principio de que Pp → ~P~p, es decir, que si está probada la verdad de una proposición no puede al propio tiempo estar probada su falsedad, la relación de accesibilidad entre mundos debe ser serial: (∀m$m’(Rmm’)). Esto significa que debe cumplirse que respecto de todo mundo existe al menos otro que es accesible al primero. Si no se impusiera esta condición, podría ocurrir que, por ejemplo, Op valiese en el mundo real y, no obstante, no valga PEp. Para que valga lo primero se requiere que en todo mundo posible accesible al mundo real sea verdad p. Si PEp no vale, ello significaría que no existe ningún mundo posible accesible al mundo real en el que p sea verdadera. Contrariamente a lo que podría parecer, estas dos afirmaciones son perfectamente compatibles, dado que el enunciado que afirma que para todo mundo posible accesible al mundo real p es verdadera es un enunciado general y condicional, que puede resultar vacuamente verdadero si es que no hay mundos deónticamente ideales respecto del mundo real. Por eso, para que Op implique PEp se requiere asumir que respecto de todo mundo posible existe al menos un mundo posible accesible.

La serialidad de la relación de accesibilidad entre mundos posibles permite justificar la validez no solo de las relaciones de subalternación en la lógica deóntica, de las creencias y de la prueba (Op → PEp, Cp → ~C~p y Pp → ~P~p), sino también las relaciones de contrariedad y subcontrariedad, pues todas ellas son proposicionalmente equivalentes entre sí, y ello se corresponde con el descubrimiento, a partir de los desarrollos de la lógica formal en la teoría de la cuantificación, de que tales relaciones valen entre los juicios categóricos bajo el presupuesto de que la clase denotada mediante el predicado F en expresiones como «Todo F es G» o «Algún F es G», no es vacía, esto es, que existe al menos un individuo que es F.

Podría considerarse la posibilidad de sistemas de lógica de la prueba más fuertes estableciendo mayores exigencias sobre la relación de accesibilidad entre mundos. Por ejemplo, si se admite como axioma el principio Pp → PPp, la relación de accesibilidad debería ser reflexiva y transitiva (∀mm’m’’ ((Rmm’ → Rm’m’’ ) → Rmm’’ )). Por simplicidad evitaremos aquí considerar la posibilidad de iterar el operador P.

Finalmente, la distancia conceptual entre prueba y verdad impulsa a tratar de aclarar las analogías y diferencias con lógicas que incorporan a la noción de verdad al cálculo formal como si fuera un operador modal adicional. Esta es la propuesta desarrollada por von Wright en diversos trabajos publicados a lo largo de casi medio siglo. En su última presentación, denominada «lógicas de la verdad» (en adelante TL, por «Truth-Logic»), von Wright (1984) intenta sistematizar diversas intuiciones lógicas aparentemente en conflicto, y para ello trata de dar cuenta del problema del papel que juegan las proposiciones que carecen de valor de verdad (lógicas intuicionistas) y aquellas proposiciones que podrían ser simultáneamente verdaderas y falsas (lógicas paraconsistentes).

En su propuesta, von Wright introduce un operador T (que puede leerse como «Es verdad que …»), que permite modalizar proposiciones ordinarias. De ese modo, Tp representa a la proposición «Es verdad que p». Dado que la falsedad de p consiste en que su negación es verdadera, T~p significa «Es falso que p» y ~Tp representa que «No es verdad que p». Diferentes axiomas permiten caracterizar a diferentes lógicas de la verdad, pero hay un núcleo común que es el siguiente:

TL0) Toda fórmula que se obtiene de las tautologías proposicionales, insertando el operador T delante de las variables proposicionales.

TL1) Tp ↔ T~~p

TL2) T(p ∧ q) ↔ Tp ∧ Tq

TL3) T~(p ∧ q) ↔ T~p ∨ T~q 31

También aquí es posible diseñar un cuadro de oposición, que ofrecerá distintas posibilidades según se añadan axiomas más fuertes o débiles a este núcleo común. Así, en caso de que se admita que una proposición p puede no ser verdadera ni falsa (~Tp ∧ ~T~p), se obtienen las relaciones de contradicción, contrariedad y subalternación características.

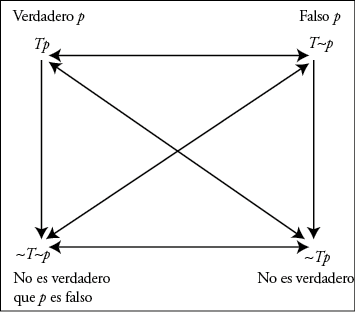
A su vez, si a este núcleo común se añade (T~p ↔ ~Tp), esto es, que una proposición p no es verdadera si y solo si es falsa, esa lógica de la verdad recoge todos los teoremas de la lógica clásica bivalente, y el cuadro de oposición se simplifica en la medida en que no hay razones para distinguir entre relaciones contrarias y contradictorias. Es interesante destacar que una lógica de la prueba puede recoger sin problemas la mayoría de los axiomas y teoremas de TL (que coincide sustancialmente con otros cálculos modales). Más adelante volveremos sobre ello, al analizar el papel de las tautologías y las leyes de distribución en la lógica de la prueba (véase sección 5).

4. Semántica de mundos posibles y estándares de prueba

Una vez que se ha dibujado una geografía de las diferentes lógicas modales y de la posible ubicación de una lógica de la prueba en este territorio formal, es importante aclarar un punto acerca de la aplicación de la semántica de mundos posibles para la lógica de la prueba. La idea de considerar que una proposición está probada si es verdadera en toda hipótesis plausible acerca de lo acontecido parece corresponderse con uno de los estándares de prueba que se consagran en el derecho, en particular el más exigente y que suele imponerse en el dominio penal de que un hecho esté probado “más allá de toda duda razonable”. Pero además de este suelen reconocerse otros estándares más débiles. Ocurre que lo que se entiende por probado en un proceso depende entre otras cosas del conjunto de criterios o estándares normativamente regulados para reputar que se ha alcanzado un cierto umbral necesario a tal fin, algo que varía en diferentes tradiciones jurídicas y en distintas áreas del derecho. Estos criterios se corresponden con la exigencia de proteger determinados bienes que se ven afectados por las decisiones judiciales, en el sentido de que cuando el bien es más valioso, como ocurre en el derecho penal (donde puede estar en juego la libertad de las personas), el estándar es más exigente. En cambio, cuando el bien resulta menos relevante (como, por ejemplo, en ciertas cuestiones patrimoniales), el estándar es menos exigente. En el derecho penal estos estándares son el producto de una ponderación del riesgo de condenar a un inocente y el de absolver a un culpable, privilegiándose la opción por la segunda alternativa. En otros sectores del derecho no existe una particular preferencia acerca de si es mejor que gane una u otra parte 32. Tres de los principales criterios utilizados en el derecho —discutidos ampliamente en la doctrina anglosajona o, más específicamente, norteamericana— son los siguientes:

a) el estándar «más allá de toda duda razonable», propio del dominio penal, al que suele asignarse un índice de probabilidad del 95 por cien;

b) el estándar de «las pruebas claras y convincentes», exigido en ciertos procedimientos civiles de particular relevancia, al que suele asignarse un índice de probabilidad de un 65 por cien, y

c) el estándar de «la preponderancia de la prueba», que es el criterio básico en derecho privado, al que suele asignarse un índice de probabilidad de más del 50 por cien.

Dados estos diferentes estándares de prueba, podría pensarse en evaluarlos como distintas variantes de la cuantificación antes propuesta sobre situaciones o hipótesis plausibles utilizando una lógica probabilística. Así, por ejemplo, se ha sostenido que, si p es consecuencia lógica de q, entonces p ∧ q sería verdadero en todo mundo lógicamente posible en que sea verdadero q, por lo cual si p no es consecuencia lógica de q pero tampoco es inconsistente con q, entonces p ∧ q sería verdadero solo en algunos mundos posibles en los que q es verdadero. Por eso se ha sugerido que, si existiera una métrica para mundos posibles, podría tomarse la relación entre el número de mundos lógicamente posibles en los que p ∧ q es verdadero y el número de mundos lógicamente posibles en los que q es verdadero para determinar el grado en que p apoya a q, y definir así la probabilidad de p dado q 33.

Aunque desde un punto de vista estrictamente formal este enfoque parece irreprochable, resulta más que controvertible que puedan asignarse significativamente valores numéricos al grado de apoyo que ciertos elementos de convicción aportan a una hipótesis sobre determinados hechos 34. Tampoco es claro cómo podría idearse una métrica para mundos posibles, lo cual parece plantear una grave dificultad para dar cuenta de distintos estándares de prueba.

Por una parte, hemos visto que la idea de cuantificación lógica sobre mundos posibles permite explicar las notables similitudes existentes entre la lógica de la prueba y otros sistemas de lógicas modales. Adicionalmente, las diferentes propiedades que pueden satisfacer las relaciones de accesibilidad entre mundos hacen posible dar cuenta de la validez de distintos principios en esos diferentes sistemas. Pero si no contamos con otra herramienta más fina que la cuantificación lógica (que solo puede discriminar entre todos, algunos y ninguno), parecería que o bien debemos renunciar a la semántica de mundos posibles para analizar la lógica de la prueba dada la imposibilidad de la primera para distinguir diferentes estándares de prueba, o bien deberíamos concluir que existe un único estándar de suficiencia probatoria.

Una posible salida a este dilema, que solo podemos aquí sugerir muy preliminarmente, es que, incluso descartando la asignación de probabilidades matemáticas a los diferentes estándares de prueba, su discriminación podría llevarse a cabo variando el dominio de la cuantificación lógica. Así, Ferrer Beltrán (2021, pp. 39-40) afirma:

… que no se pueda determinar cuánto más probable es una hipótesis que otra no impide que podamos determinar si se alcanzó por alguna de ellas un determinado resultado. Así, por ejemplo, resulta distinto exigir, para dar por probada una hipótesis acusatoria, que se hayan refutado todas las hipótesis compatibles con la inocencia (sea civil o penal), o que se haya refutado la hipótesis de la inocencia sostenida por la defensa o que solo se exija que se haya refutado esa hipótesis si la defensa aportó alguna prueba favorable a la misma.

Está claro que estas tres exigencias no son equivalentes: la primera es más fuerte que la segunda y la segunda más fuerte que la tercera. Sin embargo, la diferencia no está dada aquí por el hecho de que en cada caso se exija un umbral más alto de probabilidad o confirmación de las hipótesis en juego, sino que varía el dominio de las alternativas con las que se las contrasta: a mayor amplitud de ese dominio, mayor es la exigencia de suficiencia probatoria. Del mismo modo, la diferencia entre los estándares de prueba en materia penal y civil podría explicarse considerando que, en el primer caso, la presunción de inocencia hace que no pueda dejar de confrontarse la hipótesis acusatoria con toda hipótesis plausible en la que el imputado pueda ser inocente, en tanto que en el segundo, el principio dispositivo que atribuye a las partes la delimitación de las cuestiones a discutir y su prueba, hace que resulte mucho más circunscrito el dominio de las alternativas que el juzgador puede tomar en consideración. Creemos que este camino merece ser explorado más detenidamente.

5. Leyes de distribución, tautologías y una propuesta de axiomatización

Antes hemos visto que, en el sistema de lógica modal más débil, el operador modal puede distribuirse por el condicional. En LP tendríamos:

(14) P(p → q) → (Pp → Pq)

¿Sería aceptable ese axioma? Una respuesta afirmativa parece muy plausible ya que se adecua sin problemas a nuestras intuiciones: de la prueba de una afirmación condicional y la prueba de su antecedente debería poder concluirse que está probado su consecuente.

Sin embargo, Hart (1983, p. 109), al analizar las paradojas que surgen de ciertas reglas procesales específicas en el derecho anglosajón, como la regla que declara inaceptables los testimonios indirectos (regla del hearsay), señala:

Así, una consecuencia de la excepción bien conocida a la regla del testimonio indirecto de que la declaración es admisible como una evidencia del hecho relatado si se hace en contra de los intereses de la persona que declara, es que un tribunal puede encontrar que un hombre cometió adulterio con una cierta mujer, pero es incapaz de concluir que ella cometió adulterio con él. Un lógico podría resolver la paradoja diciendo que del hecho de que p implique q no se sigue que «está jurídicamente probado p» implica está «jurídicamente probado q».

Ahora bien, no resulta clara la razón que llevaría a un lógico a sostener tal conclusión, más allá del intento de disolver la aparente paradoja que genera esa regla procesal. Por el contrario, una lógica de la prueba parece comprometida a aceptar la distribución del operador P por el condicional, y la paradoja surge, precisamente, cuando por aplicación de esa específica regla procesal se obtiene una conclusión contradictoria.

Admitir esta distribución conduce a aceptar también una forma fuerte de distribución del operador P por la conjunción. En otras palabras, la prueba de la conjunción de p y q equivale a la conjunción de la prueba de p y la prueba de q:

(15) P(p ∧ q) ↔ (Pp ∧ Pq) 35

Estas leyes de distribución con respecto a la conjunción y el condicional, que son compartidas por diferentes lógicas modales, son ejemplos de tautologías o verdades lógicas en diversas reconstrucciones formales 36.

La noción central de la lógica (de cualquier lógica) es la de consecuencia lógica. En la medida en que la lógica suministra un criterio de racionalidad, el rechazo de una proposición que se deduce de otras que se han aceptado previamente sería algo contrario a la razón (y no solo contrario a la verdad) 37. Por ello, una concepción racionalista de la prueba parece comprometida con sostener que las consecuencias lógicas de un enunciado probatorio también están probadas.

La aceptación de que también están probadas todas las consecuencias lógicas que se siguen de un cierto enunciado probatorio es importante para analizar el papel de las tautologías, ya que una tautología es lógicamente implicada por cualquier proposición. Sin embargo, ¿es admisible tener por probadas las tautologías? Una respuesta negativa podría intentar justificarse de la siguiente manera: si la verdad de p es independiente de su prueba en un proceso judicial, entonces podría sostenerse que no es necesario comprometerse con la idea de que una tautología como, por ejemplo, (p ∨ ~p), debe tenerse siempre por probada. Por el contrario, una respuesta afirmativa parece implícita en los sistemas de regulación normativa de la prueba en el derecho, que suelen consagrar la máxima de que los hechos notorios o evidentes no requieren prueba 38. Si esto se admite, entonces con mayor razón debería admitirse que una proposición tautológica no requiere de prueba y, por ende, que todas las tautologías han de considerarse probadas. Sin embargo, es conveniente subrayar dos cosas. Por una parte, es usual señalar que las tautologías no enuncian hechos ya que no dicen nada acerca de la realidad 39, de modo que la admisión de que las tautologías están jurídicamente probadas no señala que hay razones para creer que una proposición tautológica se corresponde con los hechos del mundo, sino que es una manera de poner de manifiesto que su verdad no puede ser cuestionada y que es innecesario justificar su evidencia. Por otra parte, parece claro que, aunque ciertas tautologías son verdades evidentes, no todas las consecuencias lógicas de un conjunto de premisas son fáciles de advertir (aun cuando la relación entre esas premisas y sus consecuencias sea tautológica). Pese a ello, parece razonable mantener que las consecuencias lógicas de un enunciado probatorio también están probadas.

Por otra parte, es conveniente aceptar que las tautologías están probadas como modo de estrechar la analogía entre LP y las lógicas modales, en las que se aceptan como fórmulas válidas a OT, o NT (que señalan que las tautologías son obligatorias o necesariamente verdaderas). Sin embargo, la idea de que las tautologías proposicionales pueden ser transformadas en tautologías modales ha sido controvertida. En su artículo fundacional de la lógica deóntica von Wright (1951a) rechazaba en dicho dominio que los actos tautológicos sean obligatorios (O(p ∨ ~p)) y que los actos contradictorios están prohibidos (PH(p ∧ ~p)), sosteniendo lo que denomina el principio de contingencia deóntica (un acto tautológico no es necesariamente obligatorio, y un acto contradictorio no está necesariamente prohibido). A su juicio, si bien en la lógica de las modalidades aléticas debería aceptarse como una evidente verdad lógica que una proposición tautológica es necesaria, en la lógica de las modalidades epistémicas no debería aceptarse su análogo pues una proposición podría ser tautológica sin que lo sepamos, y termina inclinándose por estimar que la lógica deóntica debería en este punto asimilarse a la de las modalidades epistémicas porque considera que ni el lenguaje ordinario ni nuestras intuiciones lógicas de sentido común suministrarían una respuesta clara sobre si debería o no aceptarse que los actos tautológicos son obligatorios.

Contra esto Soeteman (1989, pp. 101-102) ha observado que O(p ∨ ~p) equivale a PH(p ∧ ~p), y si se rechaza la validez de esto último entonces debería admitirse la validez de PE(p ∧ ~p). Pero por lógica proposicional q equivale a q ∨ (p ∧ ~p), de modo que la fórmula PEq equivaldría a PE(q ∨ (p ∧ ~p), de lo cual se sigue, debido a la distributividad del operador PE por la disyunción, PEq ∨ PE(p ∧ ~p). Si esta fórmula fuese válida, también lo sería PEq por ser equivalente a ella, lo cual significaría que, si las proposiciones tautológicas no son obligatorias, cualquier acción estaría permitida. Este argumento resultaría concluyente para sostener el principio de que las tautologías son obligatorias si fuera correcto. Pero el argumento fracasa ya que es incorrecto derivar de la invalidez del principio O(p ∨ ~p) la validez de PE(p ∧ ~p). En verdad, lo único que se sigue de la invalidez de O(p ∨ ~p) es que su verdad es meramente contingente, esto es, que no es necesariamente verdadero, lo cual solo permite sostener que es posible que un acto contradictorio esté permitido, (PE(p ∧ ~p)) no que su verdad sea necesaria. De todos modos, Soeteman tiene razón al señalar que los principios deónticos según los cuales las tautologías son obligatorias y las contradicciones están prohibidas resultan enteramente inocuos dado que por razones lógicas no podemos sino obedecer tales obligaciones y prohibiciones.

En la mayoría de los sistemas modales se admite como regla de inferencia que de |– p se sigue |– #p, siendo # cualquier operador modal, lo que en nuestro sistema equivaldría a considerar como regla de inferencia que de |– p se sigue |– Pp (una de cuyas consecuencias es el denominado principio de hereditariedad, según el cual si p → q es un teorema, entonces también lo es Pp → Pq).

Es interesante evaluar el problema de considerar probadas las tautologías con la posible distribución del operador P por la disyunción. Si se admitiera la distributividad en la forma P(p ∨ q) ↔ (Pp ∨ Pq), y se sustituyese q por ~p, obtendríamos P(p ∨ ~p) ↔ (Pp ∨ P~p). De ello, y de la aceptación de que toda tautología ha de considerarse probada P(p ∨ ~p), se seguiría entonces (Pp ∨ P~p). Esta última expresión es la negación de (~Pp ∧ ~P~p). En otras palabras, si están probadas las tautologías proposicionales, conjuntamente con esta forma fuerte de distribución del operador P por la disyunción, se destruiría el espacio lógico para afirmar conjuntamente ~Pp y ~P~p, esto es, que pueda ocurrir que, respecto de una proposición cualquiera, no esté probado ni que es verdadera ni que es falsa.

Por lo tanto, es necesario abandonar P(p ∨ q) ↔ (Pp ∨ Pq) y buscar, como alternativa una fórmula más débil. Comencemos con la implicación de derecha a izquierda: puede demostrarse fácilmente a partir de la lógica proposicional y la regla de inferencia usualmente admitida de que si p → q es un teorema, entonces Pp → Pq es un teorema, que como p → (p ∨ q), de Pp se sigue P(p ∨ q) e igualmente de Pq se sigue P(p ∨ q). De modo que, si es verdadero Pp o es verdadero Pq, la regla de eliminación de la disyunción permite concluir P(p ∨ q).

Mucho más dudoso en cambio es admitir la implicación de izquierda a derecha de P(p ∨ q) ↔ (Pp ∨ Pq): puede estar probado que Pablo o Juan mataron a Jorge y, no obstante, no estar probado ni que Pablo mató a Jorge ni tampoco que Juan mató a Jorge. Esta intuición, sumada a la necesidad de preservar la posibilidad conjunta de ~Pp y ~P~p y a la aceptación de la prueba de las tautologías, justifica aceptar en LP solo la siguiente forma débil de distribución de P por la disyunción:

(16) (Pp ∨ Pq) → P(p ∨ q)

Si las consideraciones hechas hasta aquí son plausibles, todos los principios que hemos examinado pueden recogerse en forma axiomática en el siguiente sistema:

Vocabulario de LP:

a) Variables proposicionales p, q, r, …

b) Operador P («Está probado que …»)

c) Conectivas lógicas usuales: negación (~); conjunción (∧); disyunción (∨); condicional (→) y bicondicional (↔).

Reglas de formación:

i) Una variable proposicional es una fórmula bien formada.

ii) Una fórmula bien formada precedida por la negación es una fórmula bien formada.

iii) Dos fórmulas bien formadas vinculadas por una conectiva diádica (conjunción, disyunción, condicional, bicondicional) constituyen una fórmula bien formada.

iv) Una fórmula bien formada precedida por el operador P es una fórmula bien formada 40.

Axiomas:

LP0) Toda tautología de la lógica proposicional.

LP1) P(A → B) → (PA → PB)

LP2) PA → ~P~A

Reglas de inferencia:

R1) Regla de sustitución: Si |– A, el resultado de reemplazar uniformemente cualquier variable de A por una fórmula bien formada es un teorema.

R2) Regla de prueba: De |– A se sigue |– PA.

R3) Modus Ponens: A, A→ B |– B.

Lo notable es que, sustituyendo el operador P por el operador N, este sistema es equivalente al sistema KD de la lógica modal alética, y sustituyéndolo por el operador O, es equivalente al sistema estándar de lógica deóntica. Por otra parte, los teoremas derivables son similares a los de la lógica de la verdad TL, aunque en este último sistema —pero no en LP— se admite una forma fuerte de distribución del operador modal en la disyunción.

6. Conclusiones

Hemos visto que, asumiendo los presupuestos de una concepción racionalista de la prueba, en particular el carácter objetivo, independiente y concluyente de los enunciados de prueba, los principios lógicos que parecen validar nuestras intuiciones acerca de los enunciados probatorios permiten apreciar fuertes analogías con otros sistemas modales. Incluso es posible desarrollar una semántica de mundos posibles para la lógica de la prueba que puede dar cuenta de diferentes estándares de prueba. Esta propuesta pretende capturar una base mínima de la lógica de la prueba. La extensión de esa base mínima puede emprenderse de diversas maneras. A modo de conclusión sugeriremos una manera de abordar esa expansión, debilitando uno de los presupuestos que hemos asociado a los enunciados probatorios: su carácter concluyente. Para ello puede adoptarse una perspectiva dinámica referida a las variaciones que pueden producirse respecto de lo que se estima probado en un proceso. Así, supongamos que se decide sobre la prueba en un cierto caso de homicidio. De acuerdo con los hechos probados, se sabe que:

i) Está probado que Pablo o Juan mataron a Jorge P(p ∨ q), y

ii) Está probado que Juan no mató a Jorge P~p

A la luz de esta información, parece natural aceptar la siguiente afirmación, que es consecuencia lógica de las dos anteriores:

iii) Está probado que Pablo mató a Jorge Pq

Ahora supóngase que con posterioridad (por ejemplo, en el marco de un recurso de revisión) se obtiene:

iv) Está probado que Pablo no mató a Jorge P~q

La revisión de nuestro conjunto de enunciados probatorios originales por este nuevo enunciado probatorio deja indeterminado el resultado, pues la incorporación consistente de P~q obliga a revisar nuestro conjunto de enunciados probatorios previos (conformado por las consecuencias de P(p ∨ q) y P~p) a fin de restablecer la consistencia, lo cual puede lograrse de diversos modos. La prueba de que Pablo no mató a Jorge es compatible con considerar probado que Pablo o Juan mataron a Jorge (si descartamos que esté probado que Juan no lo hizo); también es compatible con considerar probado que Juan no mató a Jorge (si descartamos que esté probado que uno u otro lo hicieron): solo resulta incompatible con las consecuencias que se siguen de considerar probadas ambas cosas. Por ello, la incorporación consistente de P~q a nuestro conjunto originario produce dos remanentes alternativos:

R1) P~p R2) P(p ∨ q)
P~q P~q

La consecuencia de optar por R1) es que en tal caso estaríamos descartando que se encuentre probado que Pablo o Juan mataron a Jorge; en cambio, la consecuencia de optar por R2) sería que deberíamos considerar probado que Juan fue el autor del hecho. Problemas como este sugieren que se podrían obtener interesantes proyecciones de la teoría de la revisión de creencias o de lógicas derrotables para el examen de los enunciados de prueba desde una perspectiva dinámica.

BIBLIOGRAFÍA

Accatino, D. (2019). Teoría de la prueba: ¿somos todos «racionalistas» ahora? Revus, 39, 85-102.

Alchourrón, C. E. (1969). Logic of Norms and Logic of Normative Propositions. Logique et Analyse, 12 (47), 242-268.

Anderson, T., Schum, D. y Twining, W. (2005). Analysis of Evidence (2ª ed.). Cambridge University Press.

Blome-tillmann, M. (2017). «More Likely Than Not»—Knowledge First and the Role of Bare Statistical Evidence in Courts of Law. En J. A. Carter, E. C. Gordon y B. Jarvis (Eds.), Knowledge First: Approaches in Epistemology and Mind. Oxford University Press.

Cohen, L. J. (1977). The Probable and the Provable. Oxford University Press.

Cohen, L. J. (1989). Introduction to the Philosophy of Induction and Probability. Oxford University Press.

Cohen, S. (1986). Knowledge and Context. The Journal of Philosophy, 83(10), 574-583.

Cohen, S. (1988). How to Be a Fallibilist. Philosophical Perspectives, 2, 91-123.

Cohen, S. (1999). Contextualism, Skepticism, and the Structure of Reasons. Philosophical Perspectives, 13, 57-89.

Cohen, S. (2000). Contextualism and Skepticism. Philosophical Issues, 10, 94-107.

Dei Vecchi, D. (2014). Acerca de la fuerza de los enunciados probatorios: El salto constitutivo. Doxa, 37, 237-261.

Dei Vecchi, D. (2022). «Prueba sin convicción en su justa medida. Doxa, 45, 337-373.

Derose, K. (1992). Contextualism and Knowledge Attributions. Philosophy and Phenomenological Research, 52(4), 913-929.

Derose, K. (2002). Assertion, Knowledge, and Context. The Philosophical Review, 111(2), 167-203.

Fantl, J. y McGrath, M. (2002). Evidence, Pragmatics, and Justification. The Philosophical Review, 111(1), 67-94.

Fantl, J. y McGrath, M. (2007). On Pragmatic Encroachment in Epistemology. Philosophy and Phenomenological Research, 75(3), 558-589.

Fantl, J. y McGrath, M. (2009). Knowledge in an Uncertain World. Oxford University Press.

Ferrer Beltrán, J. (2005). Prueba y verdad en el derecho (2ª edición). Marcial Pons.

Ferrer Beltrán, J. (2007). La valoración racional de la prueba. Marcial Pons.

Ferrer Beltrán, J. (2021). Prueba sin convicción. Marcial Pons.

Hart, H. L. A. (1983). Problems of the Philosophy of Law. En H. L. A. Hart, Essays in Jurisprudence and Philosophy (pp. 88-120) .Oxford University Press.

Hawthorne, J. (2004). Knowledge and Lotteries. Oxford University Press.

Hawthorne, J. y Stanley, J. (2008). Knowledge and Action. The Journal of Philosophy, 105(10), 571-590.

Hintikka, J. (1962). Knowledge and Belief. An Introduction to the Logic of the Two Notions. Cornell University Press.

Ho, H. L. (2001). The Legal Concept of Evidence. En E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy, (Winter 2021 Edition). https://plato.stanford.edu/archives/win2021/entries/evidence-legal/

Kelsen, H. (1979). Teoría pura del derecho (2ª edición). UNAM.

Kripke, S. (1959). A Completeness Theorem in Modal Logic. Journal of Symbolic Logic, 24(1), 1-14.

Kripke, S. (1963). Semantical Analysis of Modal Logic I: Normal Propositional Calculi. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 9, 67-96.

Laudan, L. (2006). Truth, Error, and Criminal Law. An Essay in Legal Epistemology. Cambridge University Press.

Leibniz, G. W. (1672/1930). Elementa iuris naturalis. Otto Reichl Verlag.

Littlejohn, C. (2012). Justification and the Truth-Connection. Cambridge University Press.

Littlejohn, C. (2021). Justified Belief and Just Conviction. En Z. Hoskins y J. Robson (Eds.), The Social Epistemology of Legal Trials (1ª ed., pp. 106-123). Routledge.

Marmor, A. (2001). Three Concepts of Objectivity. En A. Marmor, Positive Law and Objective Values (pp. 112-134). Oxford University Press.

Meyer, J. J. (2001). Epistemic Logic. En L. Globe (Ed.), The Blackwell Guide to Philosophical Logic. Blackwell.

Moss, S. (2022). Knowledge and Legal Proof. En T. Szabó Gendle (Ed.), Oxford Studies in Epistemology (Vol. 7, pp. 176-213). Oxford University Press.

Pardo, M. S. (2010). The Gettier Problem and Legal Proof. Legal Theory, 16(1), 37-57.

Rescher, N. (2005). Epistemic Logic. A Survey of the Logic of Knowledge. University of Pittsburgh Press.

Rodríguez, J. L. (2021). Teoría analítica del derecho. Marcial Pons.

Rönnedal, D. (2010). An Introduction to Deontic Logic. CreateSpace.

Schauer, F. (2009). Thinking Like a Lawyer: A New Introduction to Legal Reasoning. Harvard University Press.

Soeteman, A. (1989). Logic in Law. Kluwer Academic Publishers.

Stanley, J. (2005). Knowledge and Practical Interests. Clarendon Press.

Taruffo, M. (2002). La prueba de los hechos. Trotta.

Twining, W. (2006). What is the Law of Evidence? En W. Twining, Rethinking Evidence. Exploratory Essays (pp. 192-236). Cambridge University Press.

Van ditmarsch, H., Halpern, J. Y., Van Der Hoek, W. y Kooi, B. (2015). An Introduction to Logics of Knowledge and Belief. En H. van Ditmarsch, J. Y. Halpern, W. van der Hoek y B. Kooi (Eds.), Handbook of Epistemic Logic (pp. 1-51). College Publications.

Von Wright, G. H. (1951a). Deontic Logic. Mind, 60, 1-15.

Von Wright, G. H. (1951b). An Essay in Modal Logic. North Holland.

Von Wright, G. H. (1963). Norm and Action. Routledge & Kegan, Paul.

Von Wright, G. H. (1984). Truth and Logic. En G. H. Von Wright, Truth, Knowledge and Modality (pp. 26-41). Blackwell.

Von Wright, G. H. (1996). Truth Logics. En G. H. Von Wright, Six Essays in Philosophical Logic (pp. 71-92). Acta Philosophica Fennica.

Von Wright, G. H. (2016). ¿Lógica sin verdad? Doxa, 39, 21-34.

Wigmore, J. H. (1913a). The Problem of Proof. Illinois Law Review, 8, 77-103.

Wigmore, J. H. (1913b). Principles of Judicial Proof. En J. H. Wigmore (Comp.), The Principles of Judicial Proof as Given by Logic, Psychology and General Experience and Ilustrated in Judicial Trials (pp. 3-30). Little Brown.

Wittgenstein, L. (1922). Tractatus Logico-Philosophicus. Harcourt, Brace & Co.

Zuleta, H. (2008). Normas y justificación. Marcial Pons.

---